 Photo: Lennart Ootes
Photo: Lennart OotesWesley So is not only currently the sole leader at Paris GCT, but he got there with 5 decisive games out of 6 rounds. This is an impressive display of fighting chess, especially compared to his closest rivals, Levon Aronian and Sergey Karjakin, who have 4 draws each. One of So's most impressive games was his victory against Maxime Vachier-Lagrave. It's rare that you see a queen so effectively dominated by a rook and bishop.
[pgn][Event "Grand Chess Tour Paris (Rapid)"] [Site "Paris FRA"] [Date "2018.06.20"] [Round "3"] [White "Wesley So"] [Black "Maxime Vachier-Lagrave"] [Result "1-0"] [ECO "A04"] [WhiteElo "2778"] [BlackElo "2789"] [SetUp "1"] [FEN "3q4/4rpkp/1Q1p1bp1/p1pB1p2/2P2P2/1P4P1/P2P1P1P/4R1K1 w - - 0 25"] [PlyCount "21"] [EventDate "2018.06.20"]25. Rxe7 $1 {So happily goes for the Rook + Bishop vs. Queen ending (with a couple extra pawns).} Qxb6 26. Rxf7+ Kh8 27. Rf8+ Kg7 28. Rf7+ Kh8 29. Rxf6 Qb4 30. Rxd6 Qxd2 31. Rc6 Qd4 32. Kg2 Kg7 33. Rc7+ Kh8 34. h4 h5 35. a4 {and Black resigned. MVL is in zugzwang and losing the c5 pawn, which allows So a powerful passed c-pawn.} 1-0[/pgn]
https://twitter.com/TarjeiJS/status/1009827247459618816 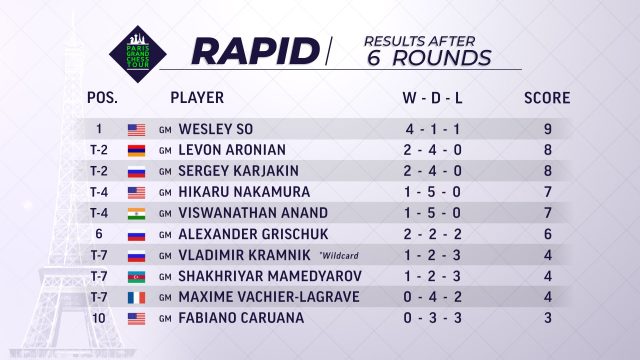 Don't miss the final day of rapid chess tomorrow at 8 a.m. EST. Watch live games and commentary by GM Yasser Seirawan, IM Jovanka Houska, GM Maurice Ashley and GM Romain Edouard on the Official Website.
Don't miss the final day of rapid chess tomorrow at 8 a.m. EST. Watch live games and commentary by GM Yasser Seirawan, IM Jovanka Houska, GM Maurice Ashley and GM Romain Edouard on the Official Website.
Categories
Archives
- January 2026 (8)
- December 2025 (27)
- November 2025 (29)
- October 2025 (39)
- September 2025 (27)
- August 2025 (29)
- July 2025 (43)
- June 2025 (25)
- May 2025 (24)
- April 2025 (29)
- March 2025 (29)
- February 2025 (20)
- January 2025 (24)
- December 2024 (34)
- November 2024 (18)
- October 2024 (35)
- September 2024 (23)
- August 2024 (27)
- July 2024 (44)
- June 2024 (27)
- May 2024 (31)
- April 2024 (51)
- March 2024 (34)
- February 2024 (25)
- January 2024 (26)
- December 2023 (29)
- November 2023 (26)
- October 2023 (37)
- September 2023 (27)
- August 2023 (37)
- July 2023 (47)
- June 2023 (33)
- May 2023 (37)
- April 2023 (45)
- March 2023 (37)
- February 2023 (28)
- January 2023 (31)
- December 2022 (23)
- November 2022 (32)
- October 2022 (31)
- September 2022 (19)
- August 2022 (39)
- July 2022 (32)
- June 2022 (35)
- May 2022 (21)
- April 2022 (31)
- March 2022 (33)
- February 2022 (21)
- January 2022 (27)
- December 2021 (36)
- November 2021 (34)
- October 2021 (25)
- September 2021 (25)
- August 2021 (41)
- July 2021 (36)
- June 2021 (29)
- May 2021 (29)
- April 2021 (31)
- March 2021 (33)
- February 2021 (28)
- January 2021 (29)
- December 2020 (38)
- November 2020 (40)
- October 2020 (41)
- September 2020 (35)
- August 2020 (38)
- July 2020 (36)
- June 2020 (46)
- May 2020 (42)
- April 2020 (37)
- March 2020 (60)
- February 2020 (38)
- January 2020 (45)
- December 2019 (34)
- November 2019 (35)
- October 2019 (42)
- September 2019 (45)
- August 2019 (56)
- July 2019 (44)
- June 2019 (35)
- May 2019 (40)
- April 2019 (48)
- March 2019 (61)
- February 2019 (39)
- January 2019 (30)
- December 2018 (29)
- November 2018 (51)
- October 2018 (45)
- September 2018 (29)
- August 2018 (49)
- July 2018 (35)
- June 2018 (31)
- May 2018 (39)
- April 2018 (31)
- March 2018 (26)
- February 2018 (33)
- January 2018 (30)
- December 2017 (26)
- November 2017 (24)
- October 2017 (30)
- September 2017 (30)
- August 2017 (31)
- July 2017 (28)
- June 2017 (32)
- May 2017 (26)
- April 2017 (37)
- March 2017 (28)
- February 2017 (30)
- January 2017 (27)
- December 2016 (29)
- November 2016 (24)
- October 2016 (32)
- September 2016 (31)
- August 2016 (27)
- July 2016 (24)
- June 2016 (26)
- May 2016 (19)
- April 2016 (30)
- March 2016 (36)
- February 2016 (28)
- January 2016 (32)
- December 2015 (26)
- November 2015 (23)
- October 2015 (16)
- September 2015 (28)
- August 2015 (28)
- July 2015 (6)
- June 2015 (1)
- May 2015 (2)
- April 2015 (1)
- February 2015 (3)
- January 2015 (1)
- December 2014 (1)
- July 2010 (1)
- October 1991 (1)
- August 1989 (1)
- January 1988 (1)
- December 1983 (1)







